微分方程式と波の重ね合わせ
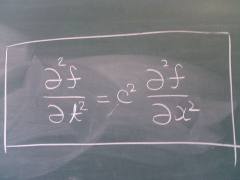
1次元の波動方程式
物体の運動をはじめとする自然現象の多くは、微分方程式、すなわち未知関数とその導関数に関する方程式によって記述することができます。物理で学ぶニュートンの運動方程式も、微分方程式の一つです。ここでは、解の存在と一意性及びその性質について詳しい解析を行っています。さらに具体的な物理現象や、人口の推移などといった様々な分野における現象を数学的にモデル化し、統一的に解明する試みを行っています。
微分方程式と波の重ね合わせ | |
 |
|
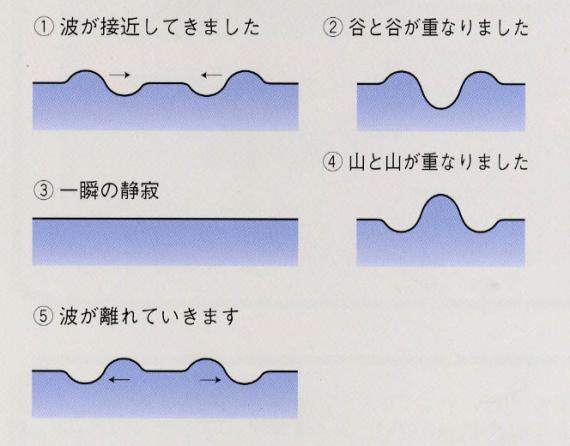
| 一見複雑に見える波の運動も、波動方程式という微分方程式で表すことができます。波動方程式が線形性という性質をもつので、波の運動には「重ね合わせの原理」 (ひとつの波動方程式のふたつの解の和が, また同じ方程式の解である) が成立します。このため、複雑な波形を、単純な振動がいくつも積み重なったものとして理解することができるのです | |