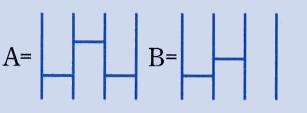
ここでは代数学の一つの対象である群(かけ算をもつもの)について紹介しましょう。かけ算といっても、数のかけ算とは限りません。
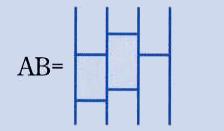
例えば、下のような４人用のあみだくじを考えてみて下さい。Aの下にBを連結したものを「AとBの積」と呼ぶことにし、A・Bで表しまょう。
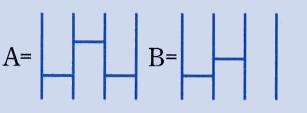
この積は普通の数の積ととてもよく似た性質をもっています。例えば、(A・B)・C＝A・(B・C) が成り立ちます。(図を描いてみて下さい)。また、下の図左のIは数でいうと１の役割をもちます (A・I＝I・A＝A)。 下の図の右のA-1は A と連結すると、「くじ」としては I と同じものになります。これは逆数に対応しています。
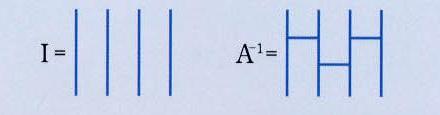
(数の積と違うところもあります。例えば A・B≠B・A です。)
ところで、次のあみだくじはどれも上のAと「くじ」としては同じものです。
横線の本数はまちまちですが、どれも奇数本です。これは偶然ではなく、実はかけ算の性質からきちんと説明がつくこと(定理)なのです。
定理：二つのあみだくじが「くじ」として同じならば、その横線の本数の偶奇は一致する。
不思議ですね。でも、このことを応用すると、例えば偶数本の横線をもつあみだくじに横線を１本をどうやって追加しても、上のIと同じ「くじ」にすることは不可能であることが説明できます。
このような「かけ算」は他にもルービックキューブの回転や行列など、実に多くのものについて考えることができます。群の理論はこれら様々に共通の(ときとして不思議な現象を引き起こす)性質を研究対象としています。
穴やループのような直観的にとらえやすい性質に注目して図形や空間を分類したり、空間に対する連続的な変形の繰り返しがもたらす効果を調べたりする分野です。
マンデルブロート集合: f(z)=z2+c という写像の繰り返しから生まれる数列が, 原点 0 を中心とした半径 2 の円から飛び出すまでに, 写像 f(z) を何回反復したか, その回数によって複素数 c に色をつけ, 複素数平面を色分けしたのが, 右の図です. シンプルな写像の繰り返しから, このような思いもよらない複雑な図形が生み出されます.